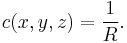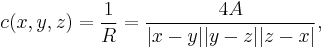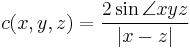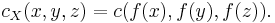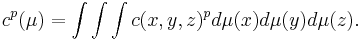Menger curvature
In mathematics, the Menger curvature of a triple of points in n-dimensional Euclidean space Rn is the reciprocal of the radius of the circle that passes through the three points. It is named after the Austrian-American mathematician Karl Menger.
Contents |
Definition
Let x, y and z be three points in Rn; for simplicity, assume for the moment that all three points are distinct and do not lie on a single straight line. Let Π ⊆ Rn be the Euclidean plane spanned by x, y and z and let C ⊆ Π be the unique Euclidean circle in Π that passes through x, y and z (the circumcircle of x, y and z). Let R be the radius of C. Then the Menger curvature c(x, y, z) of x, y and z is defined by
If the three points are collinear, R can be informally considered to be +∞, and it makes rigorous sense to define c(x, y, z) = 0. If any of the points x, y and z are coincident, again define c(x, y, z) = 0.
Using the well-known formula relating the side lengths of a triangle to its area, it follows that
where A denotes the area of the triangle spanned by x, y and z.
Another way of computing Menger curvature is the identity
where 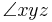 is the angle made at the y-corner of the triangle spanned by x,y,z.
is the angle made at the y-corner of the triangle spanned by x,y,z.
Menger curvature may also be defined on a general metric space. If X is a metric space and x,y, and z are distinct points, let f be an isometry from 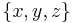 into
into 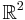 . Define the Menger curvature of these points to be
. Define the Menger curvature of these points to be
Note that f need not be defined on all of X, just on {x,y,z}, and the value cX (x,y,z) is independent of the choice of f.
Integral Curvature Rectifiability
Menger curvature can be used to give quantitative conditions for when sets in 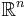 may be rectifiable. For a Borel measure
may be rectifiable. For a Borel measure  on a Euclidean space
on a Euclidean space 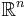 define
define
- A Borel set
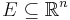 is rectifiable if
is rectifiable if 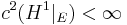 , where
, where 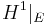 denotes one-dimensional Hausdorff measure restricted to the set
denotes one-dimensional Hausdorff measure restricted to the set  .[1].
.[1].
The basic intuition behind the result is that Menger curvature measures how straight a given triple of points are (the smaller 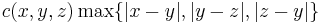 is, the closer x,y, and z are to being collinear), and this integral quantity being finite is saying that the set E is flat on most small scales. In particular, if the power in the integral is larger, our set is smoother than just being rectifiable[2]
is, the closer x,y, and z are to being collinear), and this integral quantity being finite is saying that the set E is flat on most small scales. In particular, if the power in the integral is larger, our set is smoother than just being rectifiable[2]
- Let
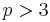 ,
, 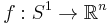 be a homeomorphism and
be a homeomorphism and 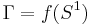 . Then
. Then 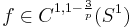 if
if 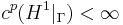 .
.
- If
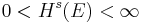 where
where 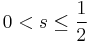 , and
, and 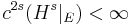 , then
, then  is rectifiable in the sense that there are countably many
is rectifiable in the sense that there are countably many 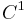 curves
curves 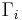 such that
such that 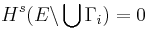 . The result is not true for
. The result is not true for 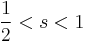 , and
, and 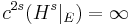 for
for 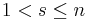 .[3]:
.[3]:
In the opposite direction, there is a result of Peter Jones[4]:
- If
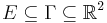 ,
, 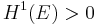 , and
, and 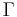 is rectifiable. Then there is a positive Radon measure
is rectifiable. Then there is a positive Radon measure  supported on
supported on  satisfying
satisfying 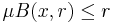 for all
for all 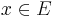 and
and 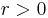 such that
such that 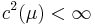 (in particular, this measure is the Frostman measure associated to E). Moreover, if
(in particular, this measure is the Frostman measure associated to E). Moreover, if 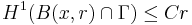 for some constant C and all
for some constant C and all 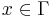 and r>0, then
and r>0, then 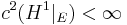 . This last result follows from the Analyst's Traveling Salesman Theorem.
. This last result follows from the Analyst's Traveling Salesman Theorem.
Analogous results hold in general metric spaces[5]:
See also
External links
- Leymarie, F. (September 2003). "Notes on Menger Curvature". Archived from the original on 2007-08-21. http://web.archive.org/web/20070821103738/http://www.lems.brown.edu/vision/people/leymarie/Notes/CurvSurf/MengerCurv/index.html. Retrieved 2007-11-19.
References
- ^ Leger, J. (1999). "Menger curvature and rectifiability". Annals of Mathematics (Annals of Mathematics) 149 (3): 831–869. doi:10.2307/121074. JSTOR 121074. http://www.emis.de/journals/Annals/149_3/leger.pdf.
- ^ Pawl Strzelecki, Marta Szumanska, Heiko von der Mosel. "Regularizing and self-avoidance effects of integral Menger curvature". Institut f¨ur Mathematik.
- ^ Yong Lin and Pertti Mattila (2000). "Menger curvature and
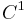 regularity of fractals". Proceedings of the American Mathematical Society 129 (6): 1755–1762. http://www.ams.org/proc/2001-129-06/S0002-9939-00-05814-7/S0002-9939-00-05814-7.pdf.
regularity of fractals". Proceedings of the American Mathematical Society 129 (6): 1755–1762. http://www.ams.org/proc/2001-129-06/S0002-9939-00-05814-7/S0002-9939-00-05814-7.pdf. - ^ Pajot, H. (2000). Analytic Capacity, Rectifiability, Menger Curvature and the Cauchy Integral. Springer. ISBN 3540000011.
- ^ Schul, Raanan (2007). "Ahlfors-regular curves in metric spaces". Annales Academiæ Scientiarum Fennicæ 32: 437–460. http://www.acadsci.fi/mathematica/Vol32/vol32pp437-460.pdf.
- Tolsa, Xavier (2000). "Principal values for the Cauchy integral and rectifiability". Proc. Amer. Math. Soc. 128 (7): 2111–2119. doi:10.1090/S0002-9939-00-05264-3.